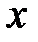Если непрерывная кривая задана уравнением 
, то площадь криволинейной трапеции, ограниченной
этой кривой, двумя прямыми 
, 
и
отрезком оси Ох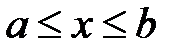 
, вычисляется по формуле:
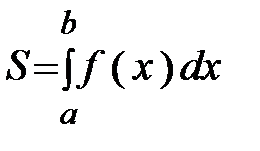. (8.16)
Это следует из геометрического
смысла определённого интеграла.
Площадь фигуры, ограниченной графиками Рисунок 52
непрерывных функций у = f 1(x) и у = f 2(x), причем f 1(x) £ f 2(x) на отрезке [ а; b ], и двумя прямыми х = а, х = b (рисунок 52), вычисляется по формуле:
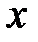
(8.17)
Пример 63. Вычислить площадь, ограниченную
параболой 
, прямыми 
и
осью Ох. Сделайте чертёж.
Решение. Построим область, ограниченную заданными
линиями (рисунок 53). Так как она представляет
собой кривролинейную трапецию на отрезке [-1; 2],
то искомую площадь вычислим по формуле (8.16): Рисунок 53
Ответ: 6 кв. ед.
Пример 64. Вычислить площадь фигуры, ограниченной линиями 
, 
.
Решение. 1) Для вычисления площади заданной фигуры сначала построим её. Первая линия, определяемая уравнением 
является параболой, ось симметрии которой параллельна оси Оу, а ветви направлены вниз.
Вершина параболы: 
, 
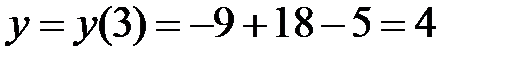, т.е. О 1(3; 4) - вершина.
Найдём точки пересечения с осью Ох:
х 1 = 1, х 2 = 5.
С Оу: х = 0; у = – 5.
Строим параболу (рисунок 54). Вторая линия, определяемая уравнением
 - прямая. Для её построения найдём
точки пересечения с осями координат:
| х | ||
| у |
Строим прямую. Область, заключенная между параболой и прямой и есть фигура, площадь которой требуется найти.
2) Определим точки пересечения линий, ограничивающих заштрихованную фигуру. Для этого решим систему, составленную из уравнений заданных линий:
.
Из рисунка 52 видно, что на отрезке [3; 5]
парабола находится выше прямой, т. е.
.
Для вычисления площади применим
формулу (8.17).
Рисунок 54
Объём тела вращения
Объём тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной кривой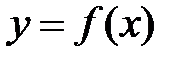 
, отрезком оси Ох 
и двумя прямыми 
и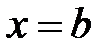 
(рисунок 55) вычисляется по формуле:
(8.18)
Объём тела, образованного вращением трапеции, ограниченной линией 
, вокруг оси Оу (рисунок 56), вычисляется по формуле:
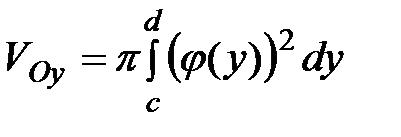(8.19)
Рисунок 55 Рисунок 56
Пример 65. Вычислить объём тела,
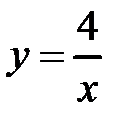
образованного вращением вокруг оси Ох
фигуры, ограниченной линиями:
Сделайте чертёж.
Решение. Построим область, которая
вращается вокруг оси Ох (рисунок 57).
ху = 4 – это гипербола. Для её построения
составим таблицу
| х | – 4 | – 2 | – 1 | |||
| у | – 1 | – 2 | – 4 |
х = 1, х = 4 – прямые, параллельные оси Оу. Рисунок 57
Так как область, которая вращается вокруг оси Ох, представляет собой криволинейную трапецию на отрезке [1; 4] оси Ох, то для вычисления объёма тела вращения применим формулу (8.18): 
.
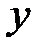
Пример 66. Вычислить объём тела,
образованного вращением вокруг оси Оу
фигуры, ограниченной линиями:
, у =1, у = 4, х = 0 (х > 0).
Сделайте чертёж.
Решение. Уравнение 
определяет эллипс. Приведём его
к каноническому виду: 
;
; 
.
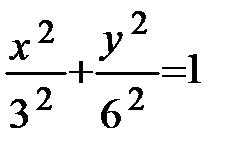а = 3 – малая полуось; b = 6 – большая полуось.
Строим эллипс (рисунок 58).
Прямые у = 1, у = 4 – параллельны оси Ох. Рисунок 58
Объём полученного тела вычисляем по формуле (8.19).
Из уравнения эллипса найдём х 2:
; 
; 
. Тогда 
и
Несобственные интегралы
Рассматривая определение определённого интеграла, как предела интегральных сумм, мы предполагали, что функция f (x) задана на отрезке 
и непрерывна на этом отрезке.
Нарушение одного из условий приводит к понятию несобственного интеграла.
Определение. Если интеграл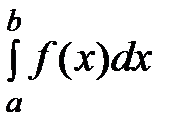 
стремится к конечному пределу при
неограниченном возрастании b, то этот предел называется не-
собственным интегралом с бесконечным верхним пределом
от функции f(x) и его обозначают символом 
.
(8.20)
В этом случае говорят, что несобственный интеграл 
сходится и равен данному пределу.
Если указанный предел не существует (в частности, если он равен бесконечности) то говорят, что интеграл расходится.
Аналогично определяется интеграл с бесконечным нижним пределом:
. (8.21)
Пример 67. Вычислить несобственные интегралы или установить их расходимость: а) 
; б) 
.
Решение. а) По определению несобственного интеграла с бесконечным верхним пределом имеем:
.
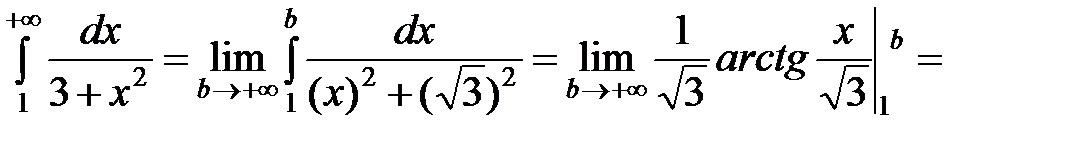
Следовательно, интеграл сходится.
б) По определению: 
, поскольку 
. Следовательно, данный интеграл расходится.