Контрольная домашняя работа. Теория вероятностей.

Расчетная работа по теории вероятностей

Задание № 1

ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫТЕОРИИ ВЕРОЯТНОСТЕЙ

1. Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта (V – номер варианта).

2. Определить испытания и элементарные события.

3. Определить исследуемое событие А и другие события.

4. Установить, какие формулы следует использовать для вычислений и выполнить последние. Вычисления произвести, по возможности точно.

Задача 1.1.

Бросают две монеты. Найти вероятность того, что:

1. на обеих монетах появится «герб»,

2. хотя бы на одной монете появится «герб»,

3. ни на одной монете не появится «герб»,

Бросают три монеты. Найти вероятность того, что:

4. на всех монетах появится «герб»,

5. хотя бы на одной монете появится «герб»,

6. только на двух монетах появится «герб»,

7. только на одной монете появится «герб»,

8. ни на одной монете не появится «герб»,

Бросают четыре монеты. Найти вероятность того, что:

9. на всех монетах появится «герб»,

10. хотя бы на одной монете появится «герб»,

11. только на одной монете появится «герб»,

12. только на двух монетах появится «герб»,

13. только на трех монетах появится «герб»,

14. ни на одной монете не появится «герб»,

Бросают игральную кость. Найти вероятность того, что на верхней грани появится:

15. четное число очков;

16. «1» или «6».

Бросают две игральные кости. Найти вероятность того, что на верхних гранях появятся очки:

17. только четные;

18. одно четное, другое нечетное;

19. сумма которых четна;

20. сумма которых нечетна;

21. сумма которых больше, чем их произведение;

22. сумма которых меньше шести;

23. сумма которых больше восьми.

Бросают три игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:

24. только четные;

25. одно четное, остальные нечетные;

26. сумма которых четна;

27. сумма которых нечетна;

28. которые все одинаковы;

29. которые все различны;

30. сумма которых делится на четыре.

 

Пример 1. Бросают три игральные кости. Найти вероятность того, что на верхних гранях появятся число очков, сумма которых делится на 5.

Решение. Событие А – сумма очков делится на 5. Вероятность события А вычисляем по формуле 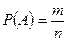. На каждой кости 6 граней и все они могут сочетаться со всеми гранями других костей, таким образом, 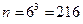. Количество m элементарных событий, благоприятствующих событию А, равно 43. Следующие комбинации очков благоприятствуют событию А:

113 122 131 136 145 154 163 212 221 226 235 244 253 262 311

316 325 334 343 352 361 366 415 424 433 442 451 456 465 514

523 532 541 546 555 564 613 622 631 636 645 654 663

Находим: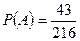

Задача 1.2.

Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке заданного слова.

Слова по вариантам:

1. ПРОГРАММА 16. ПАМЯТЬ

2. ПРОГРАММИСТ 17. ПЕРФОЛЕНТА

3. ПРОГРАММИРОВАНИЕ 18. ПЕРФОКАРТА

4. СТАТИСТИК 19. ФЕРРИТ

5. СТАТИСТИКА 20. МАГНИТ

6. СОБЫТИЕ 21. ГИСТЕРЕЗИС

7. СЛУЧАЙНОСТЬ 22. СЕРДЕЧНИК

8. ВЕРОЯТНОСТЬ 23. ПОЛУПРОВОДНИК

9. АЛГОРИТМ 24. ТРАНЗИСТОР

10. ДИФФЕРЕЦИАЛ 25. ИНТЕГРАЛ

11. ПОДПРОГРАММА 26. КАЛЬКУЛЯТОР

12. ПРОЦЕДУРА 27. ВЫЧИСЛИТЕЛЬ

13. ПРИСВАИВАНИЕ 28. ОПЕРАЦИЯ

14. УСЛОВИЕ 29. АРИФМЕТИКА

15. ПРОЦЕССОР 30. УСТРОЙСТВО

 

Пример 2. Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке слова МАТЕМАТИКА.

Решение. Элементарные события являются перестановками из 10 букв, значит n =10!. Некоторые буквы в слове повторяются (М – 2раза, А – 3раза, Т- 2раза), поэтому возможны перестановки, при которых слово не изменится, их число равно m =2! 3! 2!=24. Находим .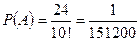

Задача 1.3.

В урне содержится К черных шаров и L белых. Случайным образом вынимают М шаров. Найти вероятность того, что в них имеется:

а) N белых шаров;

б) меньше, чем N, белых шаров;

в) хотя бы один белый шар.

Значения параметров К, L, М, и N по вариантам приведены в табл.1.

 

Таблица1

Вариант

К

L

М

N

 

Вариант

К

L

М

N

Пример 3. В урне содержится 5 черных шаров и 6 белых. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется 2 белых шара (событие А).

Решение. Общее число возможных элементарных исходов равно числу способов, которыми можно извлечь 4 шара из 11. Их число равно: 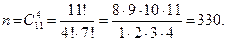Подсчитаем число исходов, благоприятствующих событию А. Среди вынутых шаров 2 белых и 2 черных; 2 белых можно взять 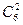способами, а 2 черных 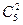способами. Следовательно, число благоприятствующих исходов равно: .

 

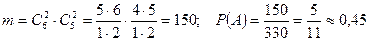Задача 1.4.

Устройство состоит из трех независимых элементов, работающих в течение времени t безотказно соответственно с вероятностями 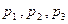. Найти вероятность того, что за время t выйдет из строя:

а) только один элемент;

б) хотя бы один элемент.

Значения параметров вычислить по следующим формулам:

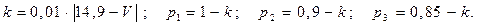
Пример 4. Устройство состоит из трех независимых элементов, работающих в течение времени t безотказно соответственно с вероятностями 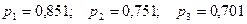. Найти вероятность того, что за время t выйдет из строя хотя бы один элемент (событие А).

Решение. Вероятность события А находим через вероятность противоположного события: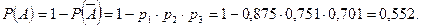

 

Задача 1.5.

В первой урне К белых и L черных шаров, а во второй - М белых и N черных. Из первой урны вынимают случайным образом Р шаров, а из второй – Q шаров. Найти вероятность того, что среди вынутых шаров: 1) все шары одного цвета;

2) только три белых шара;

3) хотя бы один белый шар.

Значения параметров K, L, M, N, P и Q по вариантам приведены в табл. 2.

Таблица 2

Вариант

К

L

М

N

Р

Q

 

Вариант

К

L

М

N

Р

Q

Пример 5. В первой урне 6 белых и 4 черных шаров, а во второй - 5 белых и 7черных. Из первой урны вынимают случайным образом 3 шара, а из второй – 2 шара. Найти вероятность того, что среди вынутых шаров:

1) все шары одного цвета;

2)только три белых шара;

3)хотя бы один белый шар.

Решение. 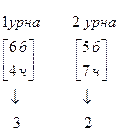1) все вынутые шары одного цвета, т.е. они либо все белые, либо все черные. Введем обозначения событий и найдем вероятности этих событий

 

2) среди вынутых шаров только 3 белых

 

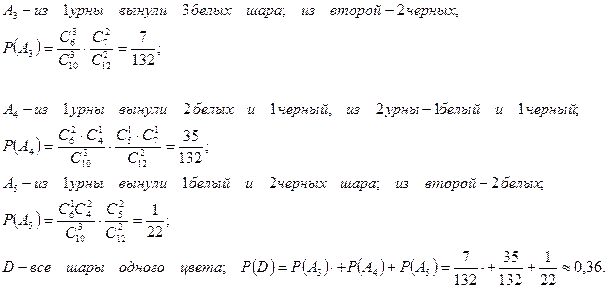
3) среди вынутых шаров хотя бы один белый шар (событие Е).

Вероятность события Е находим через вероятность противоположного события: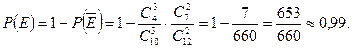

Задача 1.6.

В урне содержится К черных и белых шаров, к ним добавляют L белых шаров. После этого из урны вынимают М шаров. Найти вероятность того, что все вынутые шары белые, полагая, что все предположения о первоначальном содержании урны равновозможные.

Значения параметров К, L и М по вариантам приведены в табл. 3.

 

Таблица3

Вариант

К

L

М

 

Вариант

К

L

М

 

Пример 6. В урне содержится 4черных и белых шаров, к ним добавляют 2 белых шара. После этого из урны вынимают 3 шара. Найти вероятность того, что все вынутые шары белые (событие А), полагая, что все предположения о первоначальном содержании урны равновозможные.

Решение. Вероятность события А зависит от первоначального состава шаров в урне. Возможны следующие гипотезы:

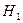- в урне было 4 белых шара, стало 6 белых;

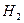- в урне было 3 белых и 1 черный шар, стало 5 белых и 1 черный;

- в урне было 2 белых и 2 черных шара, стало 4 белых и 2 черных;

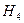-в урне был 1 белый и 3 черных шара, стало 3 белых и 3 черных;

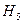- в урне было 4 черных шара, стало 2 белых и 4 черных.

Все гипотезы равновероятны, поэтому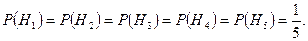

Найдем условные вероятности:

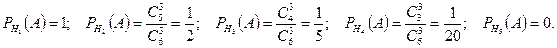
По формуле полной вероятности 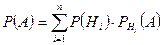находим

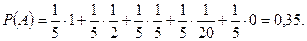
Задача 1.7.

В первой урне К белых и L черных шаров, а во второй - M белых и N черных. Из первой урны случайным образом вынимают Р шаров и опускают во вторую урну. После этого из второй урны также случайно вынимают R шаров. Найти вероятность того, что все шары, вынутые из второй урны, белые.

Значения параметров K, L, M, N, P, R по вариантам приведены в табл. 4.

Таблица 4

Вариант

К

L

М

N

Р

R

 

Вариант

К

L

М

N

Р

R

 

Задача 1.8.

В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве М₁, М₂, М₃ штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно 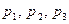. Рабочий берёт случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен первым заводом – изготовителем.

Значения параметров вычислить по следующим формулам:

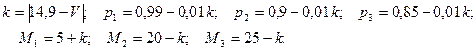
Задание № 2

ПРЕДЕЛЬНЫЕ ТЕОРЕМЫВ СХЕМЕ БЕРНУЛЛИ. ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ РАСПРЕДЕЛЕНИЯ. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

 

1. Переписать текст задачи, заменяя все параметры их значениями для вашего варианта.

2. Определить исходные данные и результаты.

3. Определить подходящие формулы вычисления и выполнить вычисления при помощи калькулятора и таблиц.

4. Построить требуемые графики.

Задача 2.1.

В каждом из n независимых испытаний событие А происходит с постоянной вероятностью р. Найти вероятность того, что событие А происходит:

а) точно G раз;

б) больше чем L раз;

в) меньше чем М и больше чем F раз;

г) меньше чем R раз.

Значения параметров n, p, G, L, M, F и R вычислить по следующим формулам:

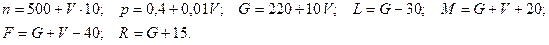
Пример 7. В каждом из500независимых испытаний событие А происходит с постоянной вероятностью р=0,4. Найти вероятность того, что событие А происходит:

а) точно220 раз;

б) больше чем 190 раз;

в) меньше чем 240и больше чем 180раз;

г) меньше чем 235раз.

Решение. а) используем локальную теорему Лапласа:

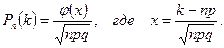
Значения функции 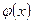находим из таблицы приложения 5, при этом нужно учитывать, что .

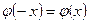Задано: n=500, p=0,4, q=0,6, k=220. Находим:

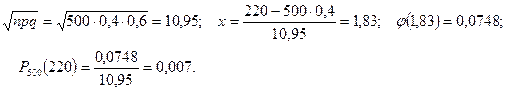
б)используем интегральную теорему Лапласа:

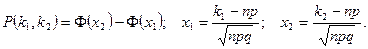
Значения функции находим из таблицы приложения 4, при этом нужно учитывать, что 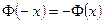и =0,5 для всех х >5.

Задано: Находим:

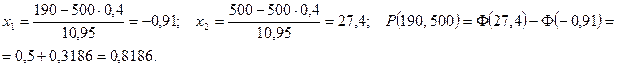
в) и г) решаются аналогично:

Задача 2.2.

На телефонной станции неправильное соединения происходит с вероятностью р. Найти вероятность того, что из n соединений произойдет:

а) точно G неправильных соединений;

б) меньше, чем L неправильных соединений;

в) больше, чем М неправильных соединений.

Значение параметров р, n, G, L и M вычислить по следующим формулам:

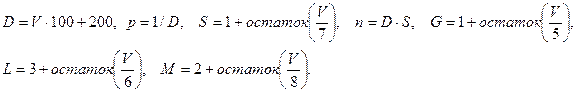
Пример 8. На телефонной станции неправильное соединения происходит с вероятностью р=0,005. Найти вероятность того, что из 200 соединений произойдет:

а) точно 1 неправильное соединение;

б) меньше, чем 3 неправильных соединений;

в) больше, чем 2 неправильных соединений.

Решение. Так как число испытаний велико, а вероятность появления события в каждом испытании очень мала, то используем формулу Пуассона:

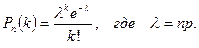
Задано: n=200, p=0,005, 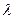=1.

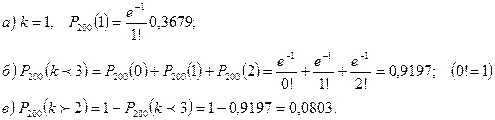
Задача 2.3.

В каждом из n независимых испытаний событие А происходит с постоянной вероятностью р. Найти вероятность того, что относительная частота этого события отличается по абсолютной величине от вероятности р не больше, чем на ε > 0.

Значения параметров n, p, ε вычислить по следующим формулам

.

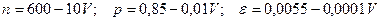Указание: воспользоваться формулой .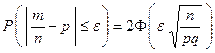

Задача 2.4.

Случайная величина Х задана функцией плотности вероятности

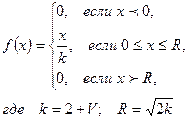
Найти функцию распределения F(x) случайной величины X. Построить графики функций f(х) и F(x). Вычислить математическое ожидание М(X) и дисперсию D(X).

Пример 9. Случайная величина Х задана функцией плотности вероятности

Найти функцию распределения F(x) случайной величины X. Вычислить математическое ожидание М(X) и дисперсию D(X).

Решение. Функцию F(x) находим по формуле: 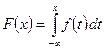. Математическое ожидание и дисперсия непрерывной случайной величины Х определяются соответственно равенствами: .

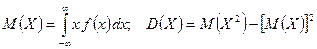Находим:

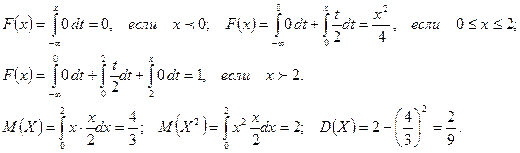
Задача 2.5.

Случайная величина Х задана функцией распределения

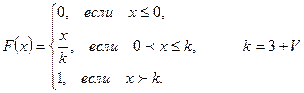
Найти функцию плотности вероятности f(х) случайной величины Х и построить графики функций f(х) и F(х). Вычислить для случайной величины Х её математическое ожидание М(X) и дисперсию D(X).

Указание: найти .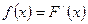

Задача 2.6.

Случайная величина Х распределена нормально. Найти вероятность того, что эта случайная величина принимает значение:

а) в интервале (а, b);

б) меньшее К;

в) большее L.

Значения параметров m, σ, a, b, K, L вычислить по формулам:

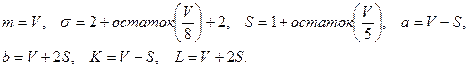
Указание. Вероятность того, что Х примет значение, принадлежащее интервалу (а, b), находим по формуле

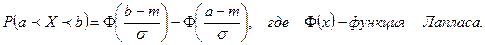(приложение 4).

 

 

Контрольная домашняя работа. Теория вероятностей.

Вариант 1

1. По движущейся цели производится три выстрела. Вероятность попадания при каждом выстреле равна соответственно 0,2, 0,3 и 0,4. Найти вероятность получить: а) три промаха; б) хотя бы одно попадание.

2. Торпедный катер атакует корабль противника, выпуская по нему одну торпеду. Вероятность попадания торпеды в носовую часть корабля равна 0,2, в среднюю - 0,3, в кормовую – 0,15. Вероятность потопления корабля при попадании в носовую часть равна 0,45, в среднюю - 0,9, в кормовую – 0,5. Определить вероятность потопления корабля противника.

3. Производится пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,4. Найти вероятность того, что событие А наступит не менее трех раз.

4. В урне 4 шара с номерами 1,2,3,4. Вынули 2 шара. Найти математическое ожидание и дисперсию случайной величины Х – суммы номеров шаров.

5. Случайная величина Х подчинена равномерному закону распределения на интервале 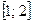. Найти математическое ожидание и дисперсию случайной величины Х.

 

 

Вариант 2

1. На огневом рубеже находятся 4 стрелка. Вероятность попадания в «десятку» при одном выстреле каждым из них соответственно равна 0,2, 0,5, 0,4, 0,7. Найти вероятность того, что при одном выстреле: а) каждый из четырех попадет в «десятку»; б) хотя бы один в «десятку».

2. По цели производится два одиночных выстрела. При одном попадании цель будет поражена с вероятностью 0,5, при двух - с вероятностью 0,8. Найти вероятность того, что в результате двух выстрелов цель будет поражена.

3. Завод отправил на базу 1000 изделий. Вероятность повреждения изделия в пути равна 0,002.

Найти вероятность того, что в пути будет повреждено не более трех изделий.

4. В партии из 20 приборов имеется 6 неточных. Наудачу отобрали 4 прибора. Найти математическое ожидание случайной величины Х – числа точных приборов среди отобранных.

5. Найти математическое ожидание случайной величины Х, распределенной равномерно в интервале (2; 8).

 

 

Вариант 3

1. При увеличении напряжения в 2 раза может произойти разрыв цепи вследствие выхода из строя любого из трех элементов с вероятностями, равными соответственно 0,3, 0,4, 0,6. Найти вероятность того, что при увеличении напряжения в 2 раза не будет разрыва цепи.

2. Элементы, изготовленные на двух предприятиях, поступают на склад готовой продукции. Три четверти от общего объема продукции, находящейся на складе, поставило 1-е предприятие и одну четверть – 2-е. Брак на 1-ом предприятии составляет 2%, на 2-ом – 4%. Найти вероятность того, что полученный со склада элемент окажется небракованным.

3. Вероятность отказа любой из 10-ти независимо работающих систем агрегата за рассматриваемый период равна 0,2. Найти вероятность того, что за данный период откажут не более 3-х систем агрегата.

4. Два стрелка делают по одному выстрелу. Вероятность попадания для первого стрелка равна 0,7, для второго – 0,9. Найти математическое ожидание и дисперсию числа попаданий в мишень.

5. Случайная величина Х подчинена равномерному закону распределения с математическим ожиданием m=3 и средним квадратическим отклонением 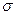=0,3. Найти плотность распределения случайной величины Х.

 

 

Вариант 4

1. По складу боеприпасов производится 3 выстрела. Вероятности попадания в склад при 1-ом, 2-ом и 3-ем выстрелах равны соответственно 0,2. 0,3 и 0,4. Для взрыва склада достаточно одного попадания. Найти вероятность того, что склад будет взорван.

2. Пиропатроны поставляются тремя заводами: 1-ый завод поставляет 50%, 2-ой – 30%, 3-ий – 20% всей продукции. Вероятность изготовления исправного пиропатрона заводами равны соответственно: 0,4, 0,8, 0,9. Найти вероятность того, что выбранный наугад пиропатрон исправен.

3. Всхожесть семян ржи составляет 90%. Найти вероятность того, что из 7-ми посеянных семян взойдет 5.

4. Из 10-ти часов, поступивших в ремонт, в общей чистке нуждаются 6 штук. Мастер, желая найти часы, нуждающиеся в общей чистке, рассматривает их поочередно и, найдя их, прекращает просмотр. Найти математическое ожидание случайной величины Х – количество просмотренных часов.

5. Все значения равномерно распределенной случайной величины лежат на отрезке 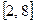. Найти вероятность попадания случайной величины в интервал (3; 5).

Вариант 5

1. Два штурмовика одновременно атакуют ракетную пусковую установку. Вероятность попадания в пусковую установку после атаки 1-го штурмовика равна 0,4, 2-го – 0,3. Найти вероятность: а) одного попадания, б) двух попаданий, в) хотя бы оного попадания в пусковую установку.

2. В трех урнах, одинаковых на вид содержатся шары: в 1-ой урне содержится 3 белых и 1 черный шар, во 2-ой – 6 белых и 4 черных, в 3-ей – 9 белых и 1 черный. Из урны, выбранной наугад, вынимают шар, который оказывается белым. Найти вероятность того, что шар вынут из 2-ой урны.

3. Вероятность появления события А в любом из 10-ти испытаний равна 0,6. Найти вероятность того, что событие А наступит не менее 2-х раз.

4. Охотник, имеющий 5 патронов, стреляет в цель до первого попадания (или пока не израсходует все патроны). Построить ряд распределения случайной величины Х –числа израсходованных патронов. Найти математическое ожидание и дисперсию случайной величины Х.

5. Случайная величина Х распределена нормально с математическим ожиданием m=10. вероятность попадания Х в интервал (10; 20) равна 0,3. Найти вероятность попадания Х в интервал (0; 10).

 

Вариант 6

1. Производится три выстрела по движущейся мишени. Вероятность попадания в мишень при первом выстреле равна 0,6, при втором – 0,75, при третьем – 0,8. Найти вероятность: а) трех попаданий, б) хотя бы одного попадания в мишень.

2. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 легкоатлета. Вероятность пройти тестирование с положительным результатом для лыжника равна 0,9, для велосипедиста – 0,8 и для легкоатлета – 0,75. Найти вероятность того, что спортсмен, вызванный случайным образом, пройдет тестирование с положительным результатом.

3. За рассматриваемый период времени среднее число ошибочных соединений, приходящееся на одного телефонного абонента, равно 8. Определить вероятность того, что для отдельно взятого абонента число ошибочных соединений будет не более двух.

4. Производятся испытания 5-ти изделий на надежность. Вероятность выдержать испытание для каждого изделия равна 0,8. Случайная величина Х – число изделий, выдержавших испытание. Найти математическое ожидание и дисперсию случайной величины Х.

5. Случайная величина Х подчинена равномерному закону распределения на интервале (2; 5). Найти математическое ожидание и среднее квадратическое отклонение случайной величины Х.

Вариант 7

1. На трех этапах подготовки изделия к функционированию вероятности появления задержек соответственно равны 0,1, 0,06 и 0,05. Найти вероятность подготовки изделия к работе без задержек.

2. Электрические приборы поставляются в магазин двумя заводами. Первый завод поставляет 60%, второй – 40% приборов. Вероятности изготовления заводами прибора, отвечающего установленным требованиям, соответственно равны: 0,95, 0,8. Найти вероятность того, что купленный стандартный прибор изготовлен первым заводом.

3. Прибор состоит из пяти независимо работающих блоков, вероятность отказа каждого из которых равна 0,3. Найти вероятность того, что число отказавших блоков не более двух.

4. Вероятность попадания в мишень для данного стрелка 0,8. За каждое попадание стрелку зачисляется 5 очков. Составить таблицу распределения случайной величины Х – числа выбитых очков при 3 выстрелах. Построить график функции распределения .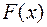

5. Случайная величина Т – время работы прибора – подчиняется экспоненциальному распределению. Среднее время работы прибора 300 ч. Найти вероятность того, что время работы прибора будет меньше 1000ч.

Вариант 8

1. В студии телевидения имеется три телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент: а) включена хотя бы одна камера; б) включены все три камеры.

2. В зоне стрельбы находятся четыре крупных цели, пять средних и одиннадцать мелких. Вероятность попадания в цель каждого типа при стрельбе соответственно равны: 0,8, 0,2, 0,1. Определить вероятность попадания в цель при одном выстреле.

3. Вероятность промаха при одном выстреле равна 0,016. Стрелок должен произвести по цели 500 выстрелов. Найти вероятность того, что он сделает не более трех промахов.

4. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны 3 детали. Найти закон распределения и функцию распределения случайной величины Х – числа стандартных деталей среди отобранных.

5. Время работы радиотехнического устройства описывается функцией показательного распределения . Найти вероятность того, что время работы устройства превысит значение его математического ожидания.

Вариант 9

1. В ящике 10 деталей, среди которых 2 нестандартные. Найти вероятность того, что в наудачу отобранных 6 деталях окажется не более одной нестандартной детали.

2. Рассматривается пять одинаковых урн. Две урны относятся к первому составу и содержат по 3 белых и 2 черных шара. Две другие урны относятся ко второму составу и содержат по 4 белых и 6 черных шаров, одна урна принадлежит к третьему составу и содержит 8 белых и 2 черных шара. Из одной урны, наугад выбранной урны, вынимают шар, который оказывается белым. Найти вероятность того, что шар взят из урны: а) первого состава; б) второго состава.

3. Вероятность того, что изделие не выдержит испытания, равна 0,001. Найти вероятность того, что из 5000 изделий более чем одно не выдержит испытаний.

4. Вероятность попадания в мишень стрелком равна 0,7. Составить ряд распределения и функцию распределения случайной величины Х – числа попаданий в мишень стрелком при 4 выстрелах.

5. Высота подрыва заряда – случайная величина, подчиненная нормальному закону распределения с математическим ожиданием, равным 1200м, и среднеквадратическим отклонением, равным 100м. Найти вероятность подрыва заряда на высоте, превышающей 1000м.

Вариант 10

1. На стеллаже библиотеки в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

2. В учебной группе 25 студентов, из них 7 учатся отлично, 10 – хорошо, 6 - удовлетворительно и 2 – неудовлетворительно. Вероятность того, что экзамен не сдаст отличник, равна 0,05, студент, учащийся на хорошо, - 0,15, студент, учащийся на удовлетворительно, - 0,3, студент, учащийся на неудовлетворительно – 0,8. Найти вероятность того, что вызванный случайным образом из состава группы студент не сдаст экзамен.

3. Вероятность попадания в цель при одном выстреле равно 0,8. Определить вероятность получения ровно трех попаданий при трех выстрелах.

4. Устройство состоит из 3 независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить ряд распределения и найти функцию распределения числа отказавших элементов в одном опыте.

5. Процент брака при изготовлении детали имеет нормальное распределение с математическим ожиданием, равным 1,5%, и средним квадратическим отклонением, равным 0,25%. Найти вероятность того, что процент брака проверяемой партии деталей лежит в пределах [1,5;2]%.

Вариант 11

1. Рабочий обслуживает 4 станка. Вероятность того, что в течении часа первый станок не требует внимания рабочего, равна 0,3, второй – 0,4, третий – 0,7, четвертый – 0,4. Найти вероятность того, что в течение часа: а) ни один станок не потребует внимания рабочего; б) хотя бы один потребует внимания рабочего.

2. На складе находится четыре монитора. Вероятность того, что монитор выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый случайным образом монитор выдержит гарантийный срок службы.

3. Найти вероятность того, что при 7 выстрела