Указания к решению задачи

Указания к контрольной работе

 

Контрольная работа выполняется по разделу «применение греко-латинских квадратов при планировании эксперимента». Студент должен выполнить одну задачу, взяв данные из таблицы в соответствии с двумя последними цифрами своего условного шифра. Работы, выполнение не по своему варианту или не в полном объеме без необходимых графиков и пояснений возвращаются для доработки.

Приступая к выполнению к контрольной работе, сначала надо изучить задание и наметить общий путь ее решения, затем перейти к выполнению отдельных его пунктов.

 

Задача

Проведены эксперименты по исследованию зависимости сопротивления рыхлению Р(Н) от числа ударов ударника ДорНИИ Су, глубины рыхления h(см), ширины наконечника S(см), угла резания α (градусы). Уровни этих переменных следующие:

 

Су = [67, 140, 300]

h = [1, 5, 10]

S = [1, 3, 10]

[30, 60, 90]

Предполагаемое уравнение регрессии

 

P = f1(Cy) * f2(h) * f3(S)* f4 (α)

 

Эксперимент проверки по плану с использованием греко-латинского квадрата

 

h1 h2 h3

Cy3 S1 α1 S2 α3 S3 α2

Cy2 S2 α2 S3 α1 S1 α3

Cy1 S3 α3 S1 α2 S2 α1

 

После эксперимента получена следующая матрица наблюдаемых значений

 

P1111 P1223 P1332

 

P = P2122 P2231 P2313

 

P3133 P3212 P3321

 

разная для каждого студента, выбирается из таблицы. Номер, обозначенный на верхней строке – предпоследняя цифра условного шифра студента. Номер, обозначенный на левой строке таблицы – последняя цифра условного шифра студента. Перед решением задачи следует внимательно изучить указания к решению задачи.

 

Таблица 1

_______________________________________________________________________

Предпоследняя цифра условного шифра студента _______________________________________________________________________

0 1 2 ________________________________________________________________________

 

580 8050 31510 560 8300 31400 560 7970 30790

1 2810 27090 20210 2890 26800 21600 2950 26940 20490

18960 18290 47100 19220 17530 47420 18210 17310 45020

 

 

570 7770 32600 580 8160 32030 570 7940 32030

2 2820 26820 20890 2870 26990 20760 2910 25750 20640

18410 17880 45760 18410 17320 47140 18720 17550 46170

 

 

550 8270 31610 570 7960 31690 580 8170 32060

3 2910 27020 21550 2930 25940 21290 2880 26430 21120

18650 18070 47100 19040 17740 45390 18640 17880 47010

 

 

580 7860 31050 550 7880 31120 590 8060 30980

4 2870 27260 21510 2760 25960 20890 2880 26030 21060

19340 17650 46820 19360 18160 44580 18710 17860 46900

 

 

570 7990 31520 550 8010 30500 590 8050 31200

5 2890 26890 21040 2890 25970 21350 2920 25800 21640

18420 18180 47010 18200 18440 47600 18730 18140 46790

 

 

560 8020 30950 550 8130 31500 560 8160 31870

6 2910 27170 21460 2800 26100 20250 2760 25570 21110

18500 18190 46460 18960 18050 44450 18660 17340 44410

 

 

550 7800 32110 560 7850 32140 550 8280 32450

7 2800 26090 21230 2850 26680 20910 2850 25910 20530

18940 18120 44640 18620 18210 46210 19110 17630 47050

 

 

580 7790 30900 550 7960 31370 550 8310 32470

8 2810 25540 21460 2970 25990 21080 2860 25890 20540

18460 18130 44940 18740 17770 44760 19320 17510 46520

 

 

580 7770 31450 570 7850 32430 560 8000 31150

9 2900 25650 21530 2830 25750 20930 2860 27110 20260

19320 18360 46810 18360 17850 47090 18750 17310 46680

 

 

570 8000 32150 560 8300 31890 580 7900 31240

2960 25770 20750 2920 27000 21290 2880 26440 21180

18890 18110 44390 19220 17780 45010 19000 18510 45670

Указания к решению задачи

 

3.1 Применение греко-латинских квадратов при планировании эксперимента

Предположим, что имеется латинский квадрат, составленный из латинских букв.

 

A B C

B C A

C A B

 

И второй латинский квадрат, составленный из греческих букв такого же порядка, что и первый.

α γ β

 

β α γ

 

γ β α

 

Наложим второй квадрат на первый

 

Aα Bγ Cβ

 

Bβ Cα Aγ

 

Cγ Aβ Bα

 

Если в полученном квадрате каждая латинская буква встречается по одному разу с каждой греческой буквой, то он называется греко-латинским. Нетрудно заметить, что полученный квадрат является греко-латинским. Не любая комбинация латинских квадратов является греко-латинским. Пусть требуется составить план эксперимента с последующим регрессионным анализом зависимости

 

R = f1(X) + f2(Y) + f3(Z) + f4(α) (1)

 

Для трех уровней переменных z и α составим греко-латинские квадраты

 

Z1 Z2 Z3 α1 α3 α2

 

Z2 Z3 Z1 α2 α1 α3

 

Z3 Z1 Z2 α3 α2 α1

 

 

Их комбинация является греко-латинским квадратом

 

 

Y1 Y2 Y3

 

X1 Z1 α1 Z2 α3 Z3 α2

 

X2 Z2 α2 Z3 α1 Z1 α3 (2),

 

X3 Z3 α3 Z1 α2 Z2 α1

 

 

к которому добавляется столбец с тремя уровнями независимой переменной X и строка с тремя уровнями независимой переменной Y.

К каждому элементу греко-латинского квадрата соответствуют уровни переменных Xi, Yj, Zk, αn, где

i, γ, k, n = [1 3]

Например, элементу греко-латинского квадрата, регламентированному на второй строке и третьем столбце соответствуют уровни переменных X2, Y3, Z1, α3.

Таким образом, греко-латинский квадрат с элементами Zк αn, с пристроенными к нему столбцами элементов Xi и строкой Yj определяют девять точек факторного пространства, т. е. являются планом эксперимента. В соответствии с этим планом получены наблюдаемые значения зависимой переменной Rijkn, представленные в матрице

 

 

R1111 R1223 R1332

 

R = R2122 R2231 R2313 (3)

 

R3133 R3212 R3321

 

которая является матрицей наблюдаемых значений.

 

Поиск значений функций f1(Xi), f2(Yj), f3(Zk), f4(αn) по аналогии с латинским квадратом производится как среднеарифметическое элементов матрицы наблюдаемых значений (3) с одинаковыми индексами соответствующих переменных.

 

Например:

 

f1(X1) = (R1111+ R1223 + R1332)/3

f1(X2) = (R2122 + R2333 + R2313)/3

f1(X3) = (R3133 + R3212 + R3321)/3

 

f2(Y1) = (R1111+ R2122 + R3133)/3

f2(Y2) = (R1223 + R2231 + R3212)/3

f2(Y3) = (R1332 + R2313 + R3321)/3

 

f1(Z1) = (R1111 + R2313 + R3212)/3 (4)

f1(Z2) = (R1223 + R2122 + R3321)/3

f1(Z3) = (R1332 + R2231 + R3133)/3

 

f1(α1) = (R1111 + R2231+ R3321)/3

f1(α2) = (R1332 + R2122 + R3212)/3

f1(α3) = (R1223+ R2313 + R3133)/3

 

По аналогии с латинским квадратом находится матрица постоянного коэффициента С

C₁₁₁₁ C₁₂₂₃ C₁₃₃₂

C = C₂₁₂₂ C₂₂₃₃ C₂₃₁₃

C₃₁₃₃ C₃₂₁₂ C₃₃₂₁

 

где С_ijkn=R_ijkn – f₁(x_i) – f₂(y_j) – f₃(s_k) – f₄(α_n) (5)

если все элементы полученной матрицы одинаковы или же незначительно отличаются друг от друга, то предполагаемая зависимость (1) справедлива, вместо которой в дальнейшем рассматривается зависимость

R = f₁(x) + f₂(y) + f₃(z) + f₄(α) + С (6),

поскольку все функции f_i определены с точностью до постоянного слагаемого.

В дальнейшем считается, что функции f_i заданы таблично при соответствующих уровнях независимых переменных x, y, z, α.

Таким образом, получены функции

R₁ = f₁(x), R₂ = f₂(y), R₃ = f₃(z), R₄ = f₄(α), (7)

т.е. задачи поиска зависимости (1) сводятся к поиску более простых четырех зависимостей (7), методика решения которых хорошо разработана

Пример:

Проф. А.Н. Зеленин исследовал зависимость сопротивлению рыхлению P от числа ударов С_y, глубина рыхления h, ширина наконечника S и угла резания α. Предложена гипотеза о зависимости между этими переменными

P = f₁(С_y)* f₂(h) *f₃(s) * f₄(α) (8),

который легко приводится к виду (1) логарифмированным

LnP = Lnf₁(c_y) + Lnf₂(h) + Lnf₃(s) + Lnf₄(α) (9)

Или

F = F₁(c_y) + F₂(h) + F₃(s) + F₄(α) (10)

где F = lnP, F₁(c_y) = lnf₁(С_y), F₂(h) = lnf₂(h),

F₃(s) = lnf₃(s), F₄(α) = lnf₄(α) (11)

 

Матрица плана эксперимента для зависимости (10) составит

h₁ h₂ h₃

C_y1 S₁ α₁ S₂ α₃ S₃ α₂

C_y2 S₂ α₂ S₃ α₁ S₁ α₃ (12)

C_y3 S₃ α₃ S₁ α₂ S₂ α₁

Где

C_y = [63 140 300]

h = [1 5 10], см

s = [1 3 10], см

α = [30 60 90]

Согласно плану проведен эксперимент и получена следующая матрица наблюдаемых значений

P₁₁₁₁ P₁₂₂₃ P₁₃₃₂

P = P₂₁₂₂ P₂₂₃₃ P₂₃₁₃ =

P₃₁₃₃ P₃₂₁₂ P₃₃₂₁

 

586 8348 32760

= 2968 27300 21700

19500 18600 47700

6.37 9.03 10.4

F = lnP = 8 10.2 9.98

9.88 9.83 10.8

По формулам (4) находим:

F₁(C_y1) = F₁(63) = (6.37+9.03+10.4)/3 = 8.6

F₁(C_y2) = F₁(140) = (8+10.2+9.98)/3 = 9.4

F₁(C_y3) = F₁(300) = (9.88+9.83+10.8)/3 = 10.2

F₂(h₁) = F₂(1) = (6.37+8+9.88)/3 = 8.08

F₂(h₂) = F₂(9) = (9.03+10.2+9.83)/3 = 9.69

F₂(h₃) = F₂(10) = (10.4+9.98+10.8)/3 = 10.4

 

F₃(s₁) = (6.37+9.98+9.83)/3 = 8.73

F₃(s₂) = (9.03+8+10.8)/3 = 9.27

F₃(s₃) = (10.4+10.2+9.88)/3 = 10.2

F₄(α₁) = (6.47+10.2+10.8)/3 = 9.12

F₄(α₂) = (10.4+8+9.83)/3 = 9.41

F₄(α₃) = (9.03+9.98+9.88)/3 = 9.63

По формуле (5) находим элементы матрицы С

Например

C₁₁₁₁ = F₁₁₁₁ – F₁(C_y1) – F₂(h₁) – F₃(S₁) – F₄(α₁) = 6.37-8.6-8.08-8.73-9.12 = -28.2

C₂₃₁₃ = F₂₃₁₃ – F₁(C_y2) – F₂(h₃) – F₃(S₁) – F₄(α₄) = 9.98-8.6-10.4-8.73-9.63 = -28.2

Вычислив остальные элементы заполним матрицу С

-28.2 -28.2 -28.2

C = -28.2 -28.2 -28.2 (13)

-28.2 -28.2 -28.2

Элементы матрицы С совпадают, что свидетельствует о справедливости зависимости (10)

В случае значительными отношениями матрицы С, вычисляется его среднее значение

C_ср = ΣC_ijkn / 9 = -28.2 (14)

Значения функции F_i и f_j в зависимости от соответствующих переменных заносим в таблицы и строим графики функции f_i, которые приведены ниже

Значения f₁(C_y)

Таблица 2

Cy
F1(Cy)	8.6	9.4	10.2
f1(Cy)=exp(F1(Cy))

 

Значения f₂(h)

Таблица 3

h,см
F2(h)	8.08	9.69	10.4
f2(h)=exp(F2(h))

 

Значение f₃(s)

Таблица 4

S,см
F3(S)	8.73	9.27	10.2
f3(S)=exp(F3(S))

 

Значения f₄(α)

Таблица 5

α
F4(α)	9.12	9.41	6.93
f4(α)=exp(F4(α))

 

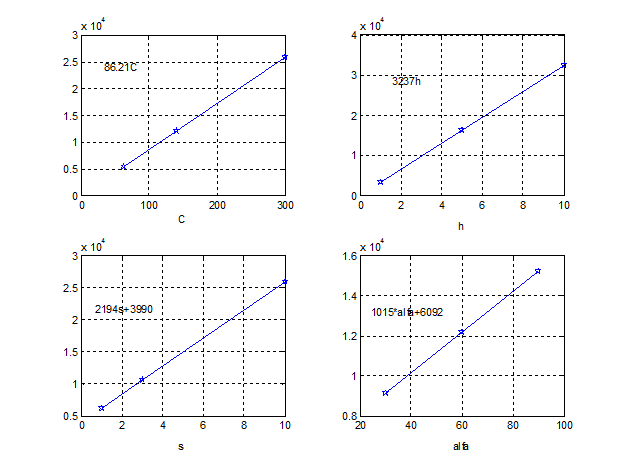
Рисунок - графики функций

Из графиков видно, что все они носят линейный характер, уравнения регрессии которых могут быть определены одним из известных способов. Например, пологая, что f₄(α) = a₀ + a₁ * α (15)

Находим

a₁ = (f₄(α₃) – f₄(α₁)) /(α₃ – α₁₎ = (15229-9138) /(90-30) = 101.5

Из уравнения (15) следует

a₀ = f₄(α₁) – a₁* α₁ = 9138-101.5*30=6092

И так получим

f₄(α) = 6092+101.5* α (16)

По аналогии из таблиц 3,2,1, имеем

f₃(S) = 3990+2194 S (17)

f₂(h) = 3237 h (18)

f₁(C_y) = 86.21 C_y (19)

Поскольку функции F_i определены с точностью до постоянного слагаемого, то функции f_i – с точностью до постоянного множителя, поэтому зависимость (8) принимает вид.

P =e^C * f₁(C_y) * f₂(h) * f₃(S) * f₄(α) (20)

Подставляем в полученное уравнение выражения (11), (13) – (16)

P = e^-28.2 * 86.21C_y * 3237h * (3990+21945) * (6092+101.5 α)

Следуя А.Н.Зеленину положим

F₄(α) = 6092+101.5(α - 90+90) = 6092+101.5(α – 90)+101.5 90 =

15227+101.5(α – 90) (21),

с учетом которого окончательно имеем

P=e^-28,2*36,21C_Y*3237h*3990(1+2194/3990*S)15227(1+101,5/19227(α-90))=

=e^28,2*36,21*3237*3990*15227C_hh(1+0,559)(1-(90-α)/150) (22)

e^-28,2*36,21*3237*3990*15227≈10

Таким образом окончательно имеем:

P=10C_Yh(1+0,55S)(1-(90-α)/150) (23)

Что совпадает с известной формулой А.Н. Зеленина для расчета сопротивлений рыхления мерзлых грунтов с точностью до множителей, учитывающих степени блокирования и затупления.