СТАТИСТИКИЕ СОВОКУПНОСТИ
Математической статистикой называется раздел математики, который занимается разработкой методов получения, описания и обработки экспериментальных данных, полученных в ходе наблюдения за массовыми случайными явлениями, с целью изучения закономерностей этих явлений.
Основные понятия
Основным понятием, которым оперирует математическая статистика является статистическая совокупность.
Статистическая совокупность – это группа, состоящая из объектов однородных относительно некоторого признака и взятых вместе в определенных границах пространства и времени.
Признаки, по которым формируется статистическая совокупность, делятся на количественные и качественные.
Пример.
К качественному признаку можно отнести наличие (да, имеется) или отсутствие (нет, не имеется) детей в семье, а к количественному – количество детей (один, два, три, четыре, …).
Для определённости статистические совокупности обозначаются прописными буквами латинского алфавита, причем чаще всего берутся буквы из последней трети алфавита – U, V, X, Y, Z. Число объектов совокупности называется ее объемом.
Статистическая совокупность, распределение которой по интересующему нас признаку необходимо изучить, называется генеральной совокупностью.
Иначе, генеральная совокупность – это совокупность всех объектов, которые являются носителями изучаемого признака.
Множество объектов, отобранных из генеральной совокупности для изучения определённого признака, называется выборочной совокупностью или выборкой.
Выборочный метод
Выборочный метод является единственно возможным, если ставится задача исследования бесконечной статистической совокупности или исследование связано с уничтожением наблюдаемых объектов (например, анализ содержимого консервных банок). Недостатком этого метода является то, что для исследования берется только часть генеральной совокупности, а значит, возможным появление ошибок. Математическая статистика дает рекомендации, как организовать отбор объектов для выборки, чтобы свести эти ошибки к минимуму, и дает методику оценки величины этих ошибок.
Основным требованием к выборке является её репрезентативность или представительность (от лат. represento – представляю). Репрезентативная выборка должна отбираться из генеральной совокупности таким образом, чтобы все объекты генеральной совокупности имели одинаковую вероятность попасть в выборку.
Опыт показывает (и подтверждается законом больших чисел), что выборка, полученная способом рандомизации (от англ. random – случай), то есть простым случайным отбором, даёт объективную картину изучаемой совокупности. Она отображает все закономерности, присущие генеральной совокупности и её широко используют при исследованиях, например, в биологии, медицине, метрологии и др. Однако, в случаях, когда генеральная совокупность неоднородна и доступность для исследователя отдельных её частей неодинакова, обеспечить репрезентативность выборки, используя механически метод рандомизации, невозможно.
Например, при изучении общественного мнения жителей большого города можно сделать ошибочные выводы, если произвести случайный опрос на улицах, так как данная выборка вряд ли будет отображать совокупное мнение всех слоёв общества (тех, кто в это время находится в аудиториях, на работе или сидит дома).
В подобных случаях для обеспечения представительности следует использовать расслоённую выборку, однако внутри каждого выделенного слоя необходимо соблюдать принцип рандомизации.
Таким образом, прежде чем приступить к отбору объектов, необходимо иметь достаточную информацию о соотношениях и особенностях, имеющих место в генеральной совокупности. Принцип рандомизации (случайности) и плановости должны, при необходимости, сочетаться, так как от этого зависит представительность выборки.
При практическом изучении генеральной совокупности чаще всего используют два основных типа выборок:
1). Повторная выборка, когда каждый элемент, случайно отобранный и исследованный, возвращается в общую совокупность и может быть вновь отобран повторно;
2). Бесповторная выборка, когда отобранный элемент не возвращается в общую совокупность.
Кроме того, выборки различаются по объему, что приходится учитывать при вычислении и анализе числовых характеристик:
1). Выборка малого объема, когда ее численность  ;
;
2). Выборка большого объема,  .
.
Описание и числовые характеристики дискретной выборки
Пусть при проведении эксперимента из генеральной совокупности объёмом N извлечена выборка Х объёмом n (n ≤ N), элементами (признаками) которой является ряд значений: х 1, х 2, …, хn, причем признак х 1 встречается в выборке m 1 раз, х 2→ m 2, …, хk → mk раз и 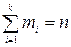 .
.
Наблюдаемые значения признака называют вариантами.
Если варианты записаны в порядке их поступления в процессе отбора, то вариационный ряд называется простым.
Если же для обнаружения закономерности при первичном анализе данные сгруппированы и записаны в порядке их возрастания или убывания, то вариационный ряд называется ранжированным (от франц. ranger – выстраивать).
Соответствующие вариантам xi числа mi называются частотами (или «весами ») признака, а их отношения к объёму выборки  – относительными частотами (где i =1, 2, …, k).
– относительными частотами (где i =1, 2, …, k).
Несложно проверить, что при этом выполняется условие  .
.
Для удобства представления и анализа данных варианты ранжированной выборки и соответствующие им mi или  заносятся в специальную таблицу:
заносятся в специальную таблицу:
| х | х 1 | х 2 | … | xи | … | xk |
| m | m 1 | m 2 | … | mи | … | mk |
| p* | p 1 | p 2 | … | pи | … | pk |
Таблицу, содержащую все сгруппированные варианты выборки и соответствующие им частоты или относительные частоты, называют статистическим дискретным рядом распределения признака (статистическим распределением выборки).
Разность между наибольшей и наименьшей вариантой называется размахом или амплитудой A вариационного ряда (варьирования признака): xmax - xmin = D Х.
Графическое изображение рядов распределения облегчает их анализ и позволяет судить о форме распределения. Для графического изображения дискретного ряда распределения используют полигон частот или относительных частот. При построении полигона частот используют координатную плоскость, на которой откладывают точки с координатами, соответствующими парам значений статистического распределения (хi; mi) или (хi; рi), а затем соединяют их отрезками прямых. Для замыкания полигона крайние точки с координатами (х 1; m 1) и (xk; mk) соединяют с точками на оси абсцисс, отстоящими в принятом масштабе от xmin = x 1 и от xmax = xn, на одно деление (рис.).
 |
Числовыми характеристиками выборки являются:
1. Выборочная средняя  .
.
2. Выборочная дисперсия 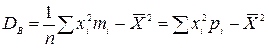 или
или 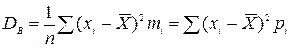 .
.
3. Выборочное среднее квадратическое отклонение 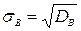 .
.
В некоторых случаях дополнительно определяют структурные средние характеристики выборки, которые также характеризуют центр распределения:
4. Мода М0 – варианта, которая встречается в выборке наиболее часто.
5. Медиана Ме – варианта, которая делит объем выборки пополам.
Очень часто они дают больше информации о центре распределения, чем средняя арифметическая величина выборки. Например, при характеристике уровня заработной платы более информативным будет показатель медианы, который говорит: половины работников предприятия получает зарплату менее Ме, другая половина имеет зарплату выше этого уровня, чем показатель – в среднем каждый работающий получает зарплату 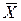 .
.
Пример.
При регистрации количества обслуживаемых на дому в 12 пунктах социальной помощи были получены результаты (данные записаны в порядке их поступления): 66, 69, 72, 70, 75, 73, 70, 71, 70, 72, 69, 70.
Составить статистическое распределение выборки.
Решение.
Ранжированный ряд более удобен для первичного анализа:
66, 69, 69, 70, 70, 70, 70, 71, 72, 72, 73, 75. Данный ряд является дискретным по своей природе, так как варианты, в данном случае это количество обслуживаемых людей, могут принимать только отдельные значения. Тогда распределение выборки, согласно определению будет иметь вид:
| Х | |||||||
| m | |||||||
| p * | 1/12 | 1/6 | 1/3 | 1/12 | 1/6 | 1/12 | 1/12 |
Графическое изображение распределения выборки – полигон частот будет иметь вид:
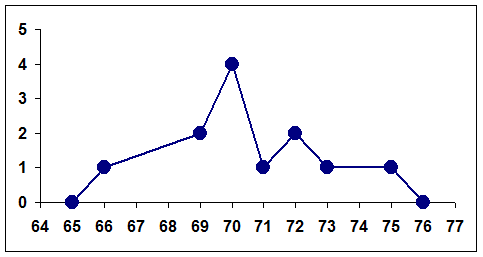 |
Вычислим выборочные характеристики:
1. Выборочная средняя
 .
.
2. Выборочная дисперсия

3. Выборочное среднее квадратическое отклонение  .
.
4. Мода 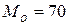 , т.к. эта варианта встречается в выборке чаще всего (m=4).
, т.к. эта варианта встречается в выборке чаще всего (m=4).
5. Медиана 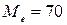 .
.

 Варианты выборки: 66, 69, 69, 70,70, 70, 70, 71, 72, 72, 73, 75.
Варианты выборки: 66, 69, 69, 70,70, 70, 70, 71, 72, 72, 73, 75.

Оценка параметров генеральной совокупности
Целью исследования, как правило, является описание всей генеральной совокупности, а не отдельной выборки, поэтому одной из основных задач статистики является оценка параметров генеральной совокупности (которые невозможно вычислить из-за отсутствия данных о всех объектах совокупности) по соответствующим параметрам выборки.
Различают точечные и интервальные оценки параметров генеральной совокупности.
Точечной называют оценку, если она оценивает одно численное значение параметра, т.е. определяется одним числом.
Интервальной оценкой называется интервал, который с заданной вероятностью накрывает оцениваемый параметр.
Статистические методы позволяют получать лишь те интервальные оценки, доверительная вероятность p которых близка к единице. Наиболее часто доверительную вероятность или степень надежности принимают равной 0,9; 0,95; 0,99; 0,999. При исследованиях доверительную вероятность обычно принимают равной 0,95. При разработке стандартов используется степень надежности 0,99.
Для получения хорошего приближения при оценке параметров генеральной совокупности П* соответствующие параметры выборочной совокупности ПВ должны отвечать двум основным требованиям: несмещённости и состоятельности.
Точечная оценка называется несмещённой, если она свободна от систематической ошибки, то есть, если математическое ожидание выборочного параметра при любых объёмах выборки «достаточно близко» или совпадает с его генеральным значением:
М(ПВ) = П*.
Точечная оценка является состоятельной, если для любого, сколько угодно малого, положительного числа e будет выполняться равенство:  .
.
Наилучшей (эффективной) называют оценку с наименьшей дисперсией.
Точечные оценки
1. Несмещённой оценкой генеральной средней является выборочная средняя, так как  , то
, то  .
.
2. Выборочная дисперсия, а следовательно, и среднее квадратическое отклонение, являются смещёнными оценками соответствующих параметров генеральной совокупности.
Это следует из свойств средней: для любой выборки сумма квадратов отклонений вариант 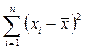 от выборочной средней
от выборочной средней  всегда меньше, чем от любого другого числа A, включая и М(Х)=m:
всегда меньше, чем от любого другого числа A, включая и М(Х)=m: 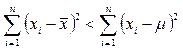 . Тогда, если выборочная дисперсия
. Тогда, если выборочная дисперсия  , то точечная оценка генеральной дисперсии σх 2 и среднего квадратического отклонения σх генеральной совокупности будет занижена, как показывает теория, в
, то точечная оценка генеральной дисперсии σх 2 и среднего квадратического отклонения σх генеральной совокупности будет занижена, как показывает теория, в  раз. Следовательно, чтобы получить несмещённую оценку (устранить систематическую ошибку), необходимо учесть это обстоятельство, то есть выборочную дисперсию необходимо умножить на
раз. Следовательно, чтобы получить несмещённую оценку (устранить систематическую ошибку), необходимо учесть это обстоятельство, то есть выборочную дисперсию необходимо умножить на  . В результате получим «исправленную» выборочную дисперсию:
. В результате получим «исправленную» выборочную дисперсию:  .
.
Следовательно, несмещенная оценка генеральной дисперсии равна:  .
.
3. Несмещенной оценкой генерального среднеквадратического отклонения является величина:  .
.
Интервальная оценка
4. Погрешностью выборочной средней является интервал, который показывает где, независимо от случайного характера выборки, будет находиться генеральная средняя или неслучайное значение величин генеральной совокупности - ее математическое ожидание:
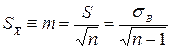 .
.
Т.о. оцененная по выборке генеральная средняя будет находиться в интервале длиной m с центром в точке математического ожидания М:
 .
.
5. Доверительным интервалом e называется интервал, в котором с заданной вероятностью будут находиться случайные величины рассматриваемого распределения в генеральной совокупности:
 ,
,
где t – коэффициент пропорциональности (коэффициент Стьюдента), величина которого зависит как от объема выборки, так и от вероятности, с которой предполагается гарантировать результат.
Величина коэффициента Стьюдента определяется по таблице в зависимости от объема выборки и величины доверительной вероятности.
Т.о., по результатам статистического анализа выборки и оценки параметров генеральной совокупности, мы гарантируем, что величины генеральной совок4упности с заданной вероятностью будут принимать свои значения в интервале:  .
.
Определение минимального объёма выборки
Как следует из выше сказанного, точность оценки параметров генеральной совокупности в большой степени определяется объёмом выборки. Но даже элементарная логика подсказывает, что неразумно стремиться к неоправданно большому числу наблюдений, если убедительный результат можно получить и при некотором минимальном объёме выборки.
Необходимая численность выборки n, отвечающая точности, с которой намечено получить средний результат, зависит от величины ошибки 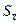 выборочной средней
выборочной средней  и может быть определена по формуле:
и может быть определена по формуле: 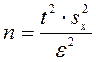 ,
,
где 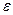 – необходимая точность оценки, t – нормированное отклонение, с которым связана та или иная доверительная вероятность p.
– необходимая точность оценки, t – нормированное отклонение, с которым связана та или иная доверительная вероятность p.
t определяется как аргумент интегральной функции Лапласа  по заданной доверительной вероятности при условии, что
по заданной доверительной вероятности при условии, что  .
.
Пример. Для определения среднего возраста студентов академии необходимо провести выборочное обследование. Предварительно установлено, что среднее квадратическое отклонение возраста студентов равно 10 годам. Сколько студентов нужно обследовать, чтобы с вероятностью 0,95 отклонение оценки от истинного среднего возраста не превышало 3 лет?
Решение: По условию задачи ε =3 года, sx =10 лет. По таблице интегральной функции Лапласа найдём значение аргумента при заданной доверительной вероятности p =0,95 t =1,96.
Итак, найдём минимальное количество необходимых для обследования студентов:  .
.
Т.о., выборка численностью 43 человека обеспечит заданную точность при оценке среднего возраста студентов.
ПЛАН СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ
Пусть в результате статистического исследования некоторой случайной величины Х были получены выборочные результаты: X = { x1, x2,..., xn}.
1. Проводим описание выборки, т.е. ранжируем ее и результат представляем в виде ряда распределения при помощи таблицы и графиков (полигон частот, гистограмма, кумулята).
2. Вычисляем выборочные характеристики:
· Выборочная средняя  .
.
· Выборочная дисперсия 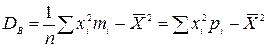 или
или  .
.
· Выборочное среднее квадратическое отклонение 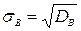 .
.
· Мода 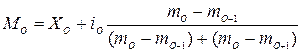 .
.
· Медиана  .
.
3. Делаем оценку параметров генеральной совокупности:
· Оценка генеральной средней  .
.
· Оценка генеральной дисперсии 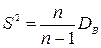 .
.
· Оценка генерального среднеквадратического отклонения  .
.
· Погрешность выборочной средней  .
.
· Доверительный интервал 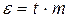 при уровне значимости α (или доверительной вероятности р).
при уровне значимости α (или доверительной вероятности р).